Growing interest in the hydrogen economy and the use of H2 as a new energy source is driving the need to understand the asset integrity of industrial systems in the presence of high-pressure molecular hydrogen. Under these conditions, electrochemical reactions usually considered to be cathodic (for example, reduction of water or H+) could change their directions, i.e., become anodic. These conversions can lead to a substantial reduction of corrosion potentials and corrosion current densities.
This article describes how OLI’s software allows users to estimate the rates of electrochemical reactions in the presence of a high amount of hydrogen in the system and, more generally, how to express the net rate of electrochemical reactions by knowing only the rate of one part (anodic or cathodic) of reactions. This type of simulation can be used to develop optimal equipment and process designs that mitigate corrosion risk during H2 production, transport and storage.
How to express the net rate of electrochemical reactions by knowing only the rate of one part (forward or backward) of reactions?
In the simplest case (in the absence of diffusion limitations) the net rate of elementary electrochemical reaction is equal to the difference between the rate of the forward reaction and the rate of the backward reaction, and can be expressed as [1]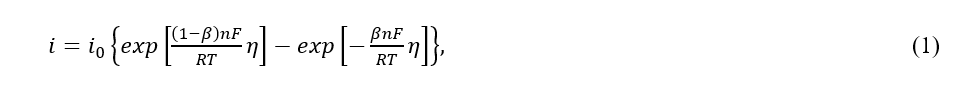
where i is the current density, i0 is the exchange current density, η = E -Er is the overpotential, n is the number of electrons transferred in electrode reaction, T is the temperature, F is Faraday’s constant, and R is the universal gas constant. Here E and Er are the electrode and reversible potentials, correspondingly.
Generally speaking, OLI’s software yields polarization curves only in one direction (anodic or cathodic) for any electrochemical reaction. However, as it is seen from Eq. (1) if we, for example, know the rate of the reaction in the cathodic direction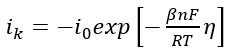 
it can be possible to calculate the rate of the reaction in the anodic direction 
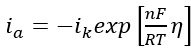and vice versa. In other words, the exchange current density, i0, determined as a function of the solution composition and the temperature allows us to calculate reaction rates in both directions.
However, there is a problem with directly applying this scheme to the case when there is a substantial amount of hydrogen in the system and particularly to the case of the important reactions:
and
The problem with these reactions is the following. The rate of these reactions in the cathodic direction in OLI’s models is presented not in the form of:
but in the form
where parameter A specifically depends on the composition and the temperature of the solution. However, the dependence of parameter A on the concentration of H2 or the partial pressure of the hydrogen is not implicitly included in A. The reason for this approach is the following.
As it was mentioned in Ref. [2], the OLI’s corrosion model is semi-empirical. i.e., some important parameters of the model are fitted to experimental data. However, the majority of available experimental data are obtained under the normal atmospheric pressure (under aerated conditions) and at least not under the addition of hydrogen to the investigated systems. It must be noted that the partial pressure of hydrogen in the air (see Figure 1) is very low (approximately 5×10-7 atm). Accordingly, the exact value of the partial hydrogen pressure (or concentration of the molecular hydrogen in the solution) is very rarely mentioned by the descriptions of the experiments. Under these circumstances it was decided, for simplicity, to include the usual value of the partial pressure of hydrogen (PH2 = 5×10-7 atm) to parameter i0 along with the corresponding value of the reversible potential term, 
to parameter A. It means that the amount of molecular hydrogen in the system is not considered as an independent parameter for describing polarization curves.
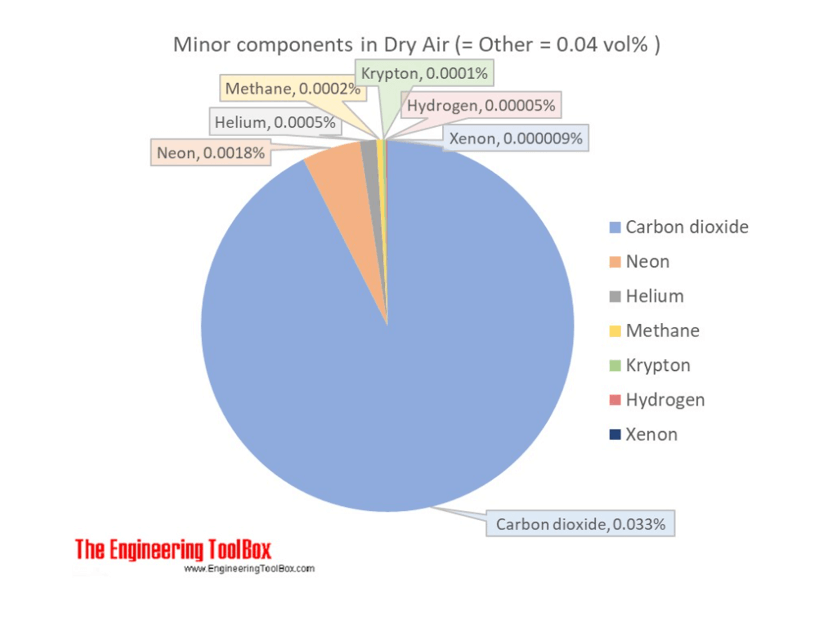
Figure 1. Typical minor components in the air. Major components: Nitrogen 78.08%, Oxygen 20.95%, Argon 0.93%.
The example below shows how the known amount of molecular hydrogen in the system can be easily considered by a user.
Example of the prediction corrosion potential and corrosion rate in the system with the substantial amount of molecular hydrogen by using OLI’s software.
As an example of the estimation of corrosion potential and corrosion rate in the system with a substantial amount of molecular hydrogen let us consider the case of the planned Belgian High-Level Nuclear Waste (HLNW) repository. This technology for the disposal of (HLNW) is based upon the concept of a “super container” comprising a carbon steel overpack containing either un-reprocessed waste (spent fuel bundles) or vitrified, reprocessed waste located concentrically with an outer stainless-steel liner (Figure 2). The corroded metal (carbon steel) surface is surrounded by two porous media (engineered barriers) between the overpack and the liner: the corrosion product and the concrete.
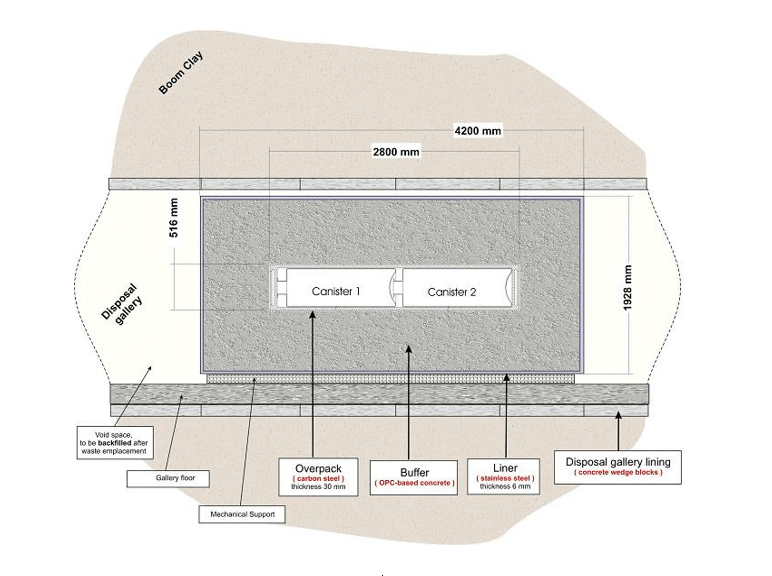
Figure 2. A longitudinal cross-section through the super container illustrating the dimensions of the various components. After Glason Sciences, Ltd [3].
Initially, the pores of the concrete are partially filled by Ca(OH)2 (sat) + 0.428 NaOH solution to yield a pH at 25 oC of 13.5. General corrosion of the carbon steel overpack in concrete pore solution has been determined to be the principal threat to the integrity of the super-container. The oxygen trapped inside the annulus will be gradually consumed by corrosion occurring at both the outer surface of the carbon steel over-pack and the inner surface of the stainless-steel envelope during the relatively short period (so-called “oxic” stage). Estimations show that the corrosion damage (thickness of the corroded metal layer) due to the initial presence of oxygen in the closed system is less than the accuracy of the known initial external radius of overpack, and, accordingly, the initial presence of oxygen can be ignored from the point of view of estimating the general corrosion damage. The main damage will occur during the “anoxic” stage the reduction of water in accordance with Eq. 3. Because the system is assumed to be closed, the hydrogen partial pressure in the annulus hydrogen gradually increases with the thickness of the corroded lay (see Figure 3).
We assume that the cathodic direction of Reaction 3 involves the reduction of the solvent (water) and hence is not mass-transfer limited. Likewise, it is also assumed that the anodic direction of Reaction 3) also is not mass-transfer limited due to the high concentrations of hydroxyl ions (in highly alkaline solutions). Moreover, we also assume that due to the small radii of the pores (in the rust and the concrete) the concentrations of H2 in the gas and the liquid phases are in equilibrium (in accordance with Henry’s law); that is, there is no diffusion limitation for transport of H2 to the overpack surface.
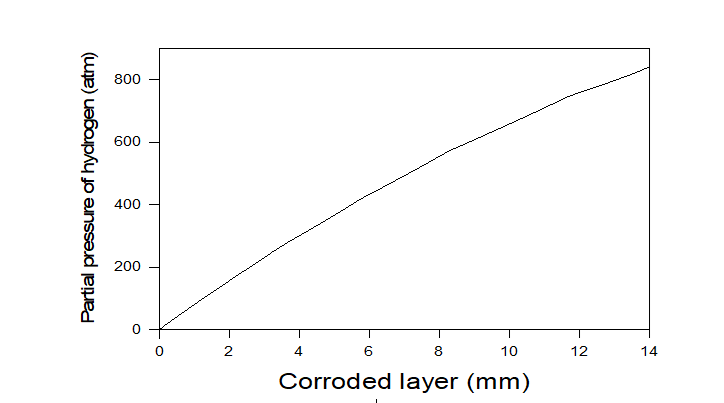
Figure 3. The partial pressure of hydrogen as a function of the thickness of the corroded layer in the overpack.
As we can see the main part of corrosion damage will be done at PH2 > 10 atm. Below we estimate corrosion potential and corrosion rate at PH2 = 10 atm and 100 atm (at T = 25 0C) by using OLI’s software.
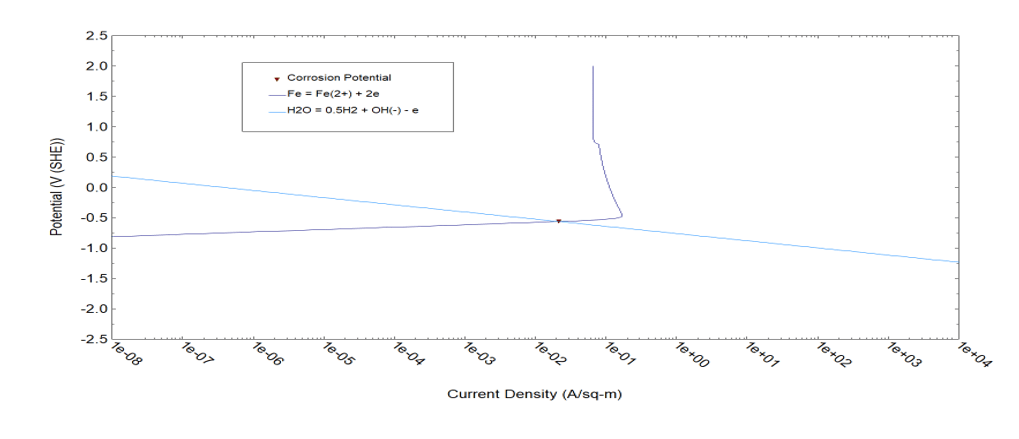Figure 4. The main polarization curves for corrosion of generic carbon steel in Ca(OH)2 (sat) + 0.428 NaOH solution to yield a pH at T = 25 oC.
Figure 4 particularly yields rate of Reaction 3 in cathodic direction. This rate can be approximated by the Dependence (5) where A = 3.842×10-7 A/m2 and β = 0.5. Accordingly. the exchange current density, i01, for Reaction 3 can be estimated as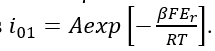 
The equilibrium potential of Reaction (3) can be estimated via the relation:
where p0 = 1 atm. At pH2 = 5×10-7 atm and pH = 13.5 we finally have i01 ≈ 0.0676 A/m2. The value of the exchange current at any other hydrogen partial pressure and at the same temperature can be estimated via the relation:
where index 1 refer to the partial pressure at pH2 = 5×10-7 atm. Here we consider that
[1, 4]. Calculations show that, for example, at pH2 = 10 atm, Er = -0.8283 VSHE and i0 = 2.02×10-4 A/m2.
At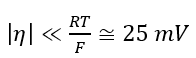 
exponents in Equation 1 can be expanded by series and this equation can be presented as:
At E=Er the dissolution rate of carbon steel is i ≈ 3×10-9 A/m2 (see anodic polarization curve for carbon steel in Figure 4). Because this value is much less than i0 we can conclude that this value can be considered as the corrosion rate (icorr ≈ 3×10-9 A/m2) and corrosion potential coincides with the reversible potential of Reaction 3 with the great accuracy. (For this case Equation 8 yields η = -3.8×10-7 V)
By analogy, at pH2 = 100 atm we have with the great accuracy Ecorr = Er = -0.8579 VSHE and icorr = 5.3×10-10 A/m2. Comparing determined values of icorr with the corrosion current density in Figure 0.0214 A/m2 shows that increasing the partial hydrogen pressure in the system can lead to the substantial reduction of the corrosion current density (by orders of magnitude). This can be considered as the good news from the point of view of the corrosion integrity of the repository.
Remark
In more general case, in the presence of transport (diffusion limitations) the current densities are described by the Generalized Butler-Volmer Equation (GBVE):
Where ila and ilc are the limiting currents for the anodic and cathodic directions, correspondingly. In this case, the exchange current density, determined by obtaining OLI’s software in one direction (and recalculated, if necessary, by using Eq. 7 at the presence of the substantial amount of the molecular hydrogen) can be also used for estimating the rate of the electrochemical reactions in both directions.
Summary
- In the case when a substantial amount of molecular hydrogen is present in the system the recalculation of the exchange current density can be performed via Equation 7.
- The increase of the amount of molecular hydrogen in the system leads to the decreasing of the corrosion potential and corrosion current density.
- When a sufficiently high amount of hydrogen is present in the system under anoxic conditions (or in the absence of other than oxygen dominant oxidizer) the corrosion potentials are equal (with great accuracy) to the reversible potential of Reaction 3 in alkaline solution (or Reaction 2 in the neutral or acidic solutions).
References
- Newman and K. E. Thomas-Alyea, Electrochemical Systems, 3rd Ed., J. (Hoboken NJ, Wiley & Sons) 2004.
- Anderko, “Modeling of Aqueous Corrosion,” in Volume 2, chapter 2.38 of Shreir’s Corrosion, 4th edition, edited by R.A. Cottis, M. Graham, R. Lindsay, S.B. Lyon, T.J.A. Richardson, J.D. Scantlebury, and H. Stott, Elsevier, Amsterdam (2010), pp. 1585-1629.
- Galson Sciences Ltd., “Supercontainer Phase 2: Input Data and Boundary Conditions to Support Modelling Studies of the Belgian Supercontainer Design for HLW Disposal”, Report to ONDRAF-NIRAS, March 1, 2005.
- D. Macdonald, J. Qiu, Y. Zhu, J. Yang, G. R. Engelhardt, Corrosion of rebar in concrete, Part I: Calculation of the corrosion potential in the passive state, Corr. Sci, 177 (2020) 09018.