Predicting the environmental sustainability of nuclear waste repositories in Sweden using the OLI Platform

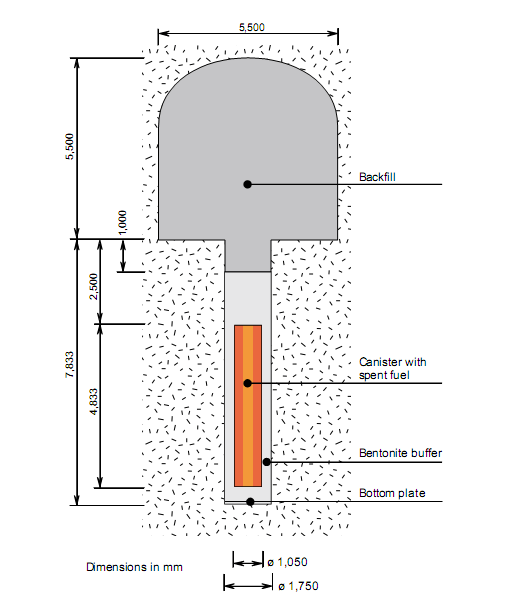
Sweden’s three nuclear plants cover around 40 % of the country’s electricity needs. The spent fuel is stored temporarily at the CLAB facility, but a deep repository has to be built for permanent disposal. It is planned that the copper canister (5 cm thick) will be emplaced at depth of several hundred meters (where there is no oxygen in the ground water). The canisters will be encased in compacted bentonite, which will be used as a buffer (see Figure 1). The main role of the buffer is to prevent the surrounding environment from the penetration of the radioactive species from the canister containing highly radioactive waste, should the canister be ruptured. However, the buffer also prevents the copper surface of the canister from corrosion. Bentonite is chosen due to its swelling properties because cracks may appear in the surrounding rocks and these cracks need to be plugged.
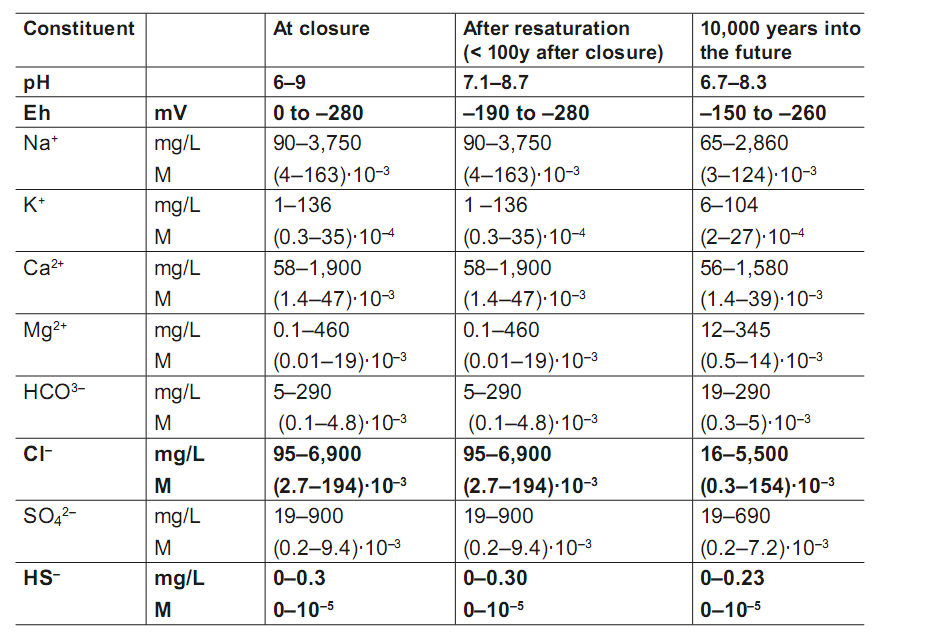
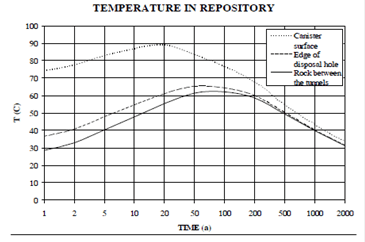
The expected composition of groundwater is shown in Table 1. Figure 2 yields predicted variation of temperature as a function of time near the canister surface.
OLI software allows us to find out the most dangerous component in the ground water from the point of view of copper corrosion – HS- ions. Thus, for example, OLI software [1] predicts that corrosion rate of copper in 0.1 m NaCl + 0.01m NaSO4 at T = 25 °C under static conditions equals 1.59×10-6 mm/y whereas after addition only 10-5 m NaHS corrosion rate increases by 3 orders of magnitude (1.95×10-3 mm/y). The calculations for the latter case are illustrated by Figure 3.
There are two models for describing copper corrosion in the presence of HS- ions. In accordance with the first model copper metal loses much of its corrosion resistance in the presence of sulphide ion and other sulfur-containing species with the metal forming Cu2S [2]:
![]() (1)
(1)
In this case the reduction of water becomes a viable partial cathodic reaction thereby giving rise to the corrosion of copper in anoxic environments.
On the other hand, if the compound Cu2S dissolves relatively fast, the total anodic reaction can be rewritten as [3]:
![]() (2)
(2)
In this case the reaction 2HS^-+2e^-→H_2+2S^(2-)is considered to be the main cathodic reaction.

It would be worthwhile to find an upper estimate of the loss of copper from the wall of the container and an upper estimate of the corrosion potential during over 100,
As we can see the upper estimate in both cases reduces to the estimation of the limiting flux density of HS- ions (see, for example, Figure 3) from bentonite/rock interface to the coper surface (copper bentonite interface). It is evident that the most important parameter for calculating the limiting current density in the porous (bentonite) media is the effective diffusion coefficient of i-th species:
D_(e,i)=ε δ/τ^2 D_(w,i) (3)
Here, ε is the porosity and Dw,i is the diffusion coefficient in free water. The tortuosity τ reflects that the diffusion of the diffusing species has to take a longer path than a straight line and the constrictive factor δ reflects the effects of the narrowing and widening of the pores. Direct measurements show that the geometrical factor, δ/τ, in bentonite follows Archie’s law, i.e. δ/τ^2=ε^n, where the empirical factor n = 0.9 [4]. Accordingly,
D_(e,i)=ε^(1+n) D_(w,i)=ε^1.9 D_(w,i) (4)
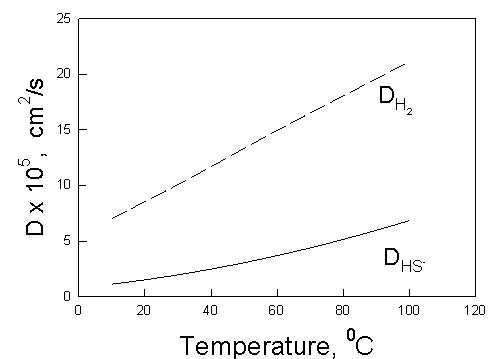
Figure 4 shows the diffusion coefficient of HS- and H2 in dilute aqueous solutions as a function of temperature. The calculations were made by using OLI’s models and software [5].
The mass balance equation for HS- ions in polar coordinates has the following form:
![]() (5)
(5)
The initial and boundary conditions are as follows: at t = 0 and at r = rc, at r = rb, where is the concentration of HS- ions in the groundwater in the pores of the rock. Here rc is the outer radius of the copper container and rb is the outer radius of the bentonite (bentonite/rock) border.
Equation (5) was solved numerically assuming that temperature inside bentonite can be found on the base of Figure 3. After finding the limiting flux of HS- to the canister (copper) surface, we can be easily find the maximum possible corrosion current density and the maximum possible thickness of corroded layer (by applying Faraday’s law) as a function of time (see, as examples, Figures 5 and 6).
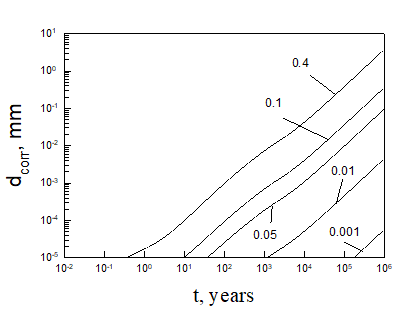
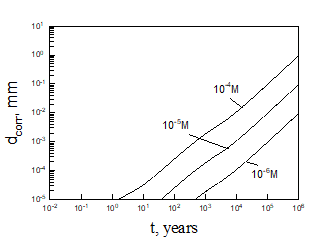
Calculations show that the general corrosion damage in the repository is predicted not to be substantial, at least over a storage time of 106 years if no catastrophic events take place in the repository. However, if the bentonite buffer is destroyed for any reason, and does not act as an engineered barrier (e.g., when containers are washed by ground water), it can occur that the ready access of sulphide species to the canister surface can destroy the canister within less than 105 years. Thus, for example, calculations yield that copper canister with the thickness of 5 cm will be destroyed within 3424 years in 0.1 m NaCl + 0.01m NaSO4 +10-5 m NaHS solution at T = 10 0C under complete agitations conditions and within 37116 years under static conditions. However, the catastrophic destruction of the confined bentonite buffer is an inconceivable event and these calculations should be regarded as being illustrative only.
OLI’s platform is also used for predicting environmental sustainability in planned nuclear waste repository in Belgian (ONDRAF project).